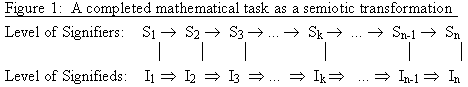

This is a speculative exploration of the semiotics of mathematical text which draws upon diverse sources from philosophy, mythology and literary criticism. It represents an incomplete opening of a line of research, and its tentativity is reflected both in the content and in the adoption of a dialogical style. This allows the counterpoising of different themes without offering a tidy synthesis or end.
A social constructivist account of proof as a means of persuading the mathematical community is now widely accepted (Ernest 1991, Tymoczko 1986, Hersh 1993). Gaining acceptance from expert judges who act as gatekeepers in mathematics is thus the key epistemological role of proof. But for those who accept that the traditional absolutist role of logic has been dethroned, a question remains. What does the reader of mathematical proof experience that convinces her or him to accept the theorem, instead of flawless logic alone? What psychological processes are involved in the reader experiencing the text? What does the reader of a mathematical proof experience that convinces him or her to accept it? Given that the proof is a text, how does the reader engage with that text decisively?
This paper offers a tentative social constructivist and semiotic-based exploration of proof, which is intended to also describe the way some learners of mathematics interact with texts and tasks.
First of all every reader of mathematical text or proof approaches the task with a long and complex personal history, and within a socio-cultural context or discursive practice. Every sign, fragment of text, or task in mathematics has two intertwined and inseparable in all but name aspects: that of signifier and signified. My claim is that the realm of signifieds is an imaginary, textually-defined realm, which via processes of intuition ultimately forms the platonic universes that mathematicians' thoughts inhabit. Part of any mathematics learner's or mathematician's role in interpreting a mathematical text is to imagine a miniature math world signified by the text. But in reading a proof or carrying out a classroom task, the reader is following (or accomplishing) the transformation of that text. In doing this, according to Rotman's (1993) analysis the mathematician is carrying out imagined text based actions. In reading a proof, these involve imagined actions coupled with transformations of text which have a cyclic pattern. The beginning is the announcement of the endpoint, the theorem to be proved. This is followed by an imagined voyage through text and underlying math-world, until the endpoint is reached. (For the learner undertaking a mathematical task, the beginning is a pointer to the endpoint – a directive to 'solve' the problem: this is both to undertake a quest, and to transform a text.)
According to Rotman (1993) the mathematician alternates his identity or subjectivity between that of the mathematician and his agent: the imagined skeletal representation of self - like the moving fingertip on a map retracing a journey. This representation of self - like the turtle in Logo - or the hero/agent in a computer adventure game - traces out a journey of adventure, analogous to the universal 'hero with a thousand faces' in Campbell's (1956) mythic cycle.
In the paper I explore this analogy, and also that between algorithm and proof, and argue that the latter pair have more in common than is often acknowledged. Thus involvement in the procedures of school mathematics provides an apprenticeship for the future mathematician, in which she learns to project her self into the script, programme, or imagined math-world of the mathematical task. However my conjecture is that the future mathematician learns (1) to obey the imperatives in mathematical text, (2) to write such mathematical texts, and (3) to jump out of the script (i.e. change role from subjected agent to mathematician) and critique it. However many others learn only to be a regulated subject (i.e.1 above), carrying out on paper and in mind what it needs only a machine to do.
It has been remarked that in modern Anglo-Saxon thought there are two incommensurate cultures, that of science and that of the humanities and literary thought (Snow 1959).
However much modern continental European philosophy and post-modernist thought reject this division and parallel dichotomies such as the following: absolute logical knowledge versus fallible empirical knowledge, representational language versus poetic language, mind and rational thought versus body and feeling, word versus deed, Logos versus Mythos.
What has emerged from such perspectives is the pre-eminence of language and narrative, concretely realised in the world. According to Lyotard (1979) all scientific knowledge must present itself as a narrative to legitimate itself.
From such a perspective, all mathematical and scientific knowledge, mathematical proof in particular, are discursive forms, are narratives. Thus it is appropriate to apply the tools of linguistics, semiotics and literary analysis to mathematics. Thus I pose the questions: What tales do mathematical proof narratives tell? Who is the teller of mathematical tales and who is the listener? What syntactical and linguistic forms are employed in the story and how do they relate to the content of the tale? If mathematics is written in sentences what are their subjects, objects and verbs? How are the ideas of necessity and certainty of mathematical knowledge formed and expressed? How is the platonic realm of mathematical forms and objects created and sustained by mathematical narratives?
Young (1987) proposes a structured theory of narrative based on the frame analysis of Goffman, Natanson and others. She locates narratives in the realm of conversation, and regards them as existing on two levels, or in two frames. First there is the storyrealm, which is the narrative text itself. Second, there is the Taleworld, the framed world of meanings created, referred to and traversed in the narrative. Each of these realms exists within a frame, which is indicated by opening and closing markers signalling the move in or out of the frame. According to her theory, the following common structure is shared by narratives. Within the realm of conversation, a 'preface' announces a coming narrative, and an 'opening' indicates a move into the storyrealm, where the narrative begins. Following this a 'beginning' indicates a shift into the Taleworld, where the story unfolds until it reaches its conclusion or 'end'. This signals a move back out of Taleworld into the storyrealm. A further move out of the storyrealm is signalled or framed by a 'closing', and back in the realm of conversation a 'coda' puts a final marker to show that the storyrealm is closed.
This structure suggests both a symmetry and a cyclic structure to narratives, which begin and end with a single narrator in the realm of conversation. From this start, they move into the Taleworld, cross the threshold into the storyrealm, traverse the tale itself, then cross back into storyrealm, and before finally returning into the realm of conversation. There is a strong symmetry (reflectional symmetry in time) with matched openings and closings throughout. This symmetry, with the consequent return to the original realm of conversation, gives the structure an implicit circularity.
This theoretical account suits that of mathematical proof well in several ways. A semi-formal or informal proof is a narrative, which begins at the level of language (the signifier level), moves to that of meanings (the level of signifieds), and then finally returns to the level of language at the end. It is also a cyclic narrative, as I shall further elaborate below. There are markers in proofs indicating openings or beginnings and closings or ends. Thus there is a good fit between the patterns. One are of difference is that a semiformal proof may alternate between the level of language and that of meanings more than once, unlike the story pattern. But that could easily be generalized; and indeed modern novels and film narratives often alternate between the levels of medium and content several times.
A mathematical proof or problem-solving task in mathematics (see Ernest 1993) may thus be seen to have a similar structure, comprising a sequence of signs which can be understood both as a sequence of textual transformations on the level of signifiers (the storyrealm) and of conceptual transformations on the level of signifieds (the Taleworld).
A simplified diagram illustrating these transformations is shown in Figure 1.
Figure 1: A completed mathematical task as a semiotic transformation
I shall leave aside tasks and focus on proof here. In mathematical terms, this transformational 'narrative' can be understood as have a cyclic structure because it begins with the statement of theorem to be proved, and ends by returning to the theorem, but this time having reached it with a proof, having provided an epistemological warrant for it. Mathematically, we can understand a mathematical proof as having the following structure
The Cyclic Pattern of Mathematical Proof
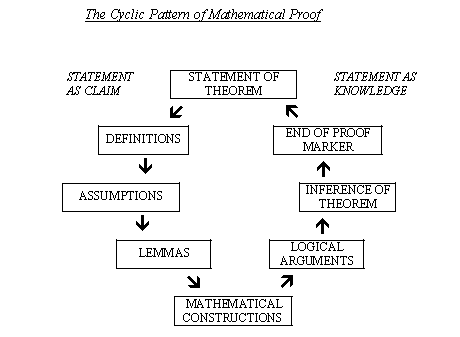
The stages in the journey are:
Statement of theorem,
Assumptions,
Definitions,
Lemmas,
Mathematical constructions
'Logical' arguments,
Inference of theorem
End marker (Halmos bar)
Johnson (1987) argues that many of our most abstract ideas originate in a range of basic bodily experiences and experiential conceptions. He suggests that the presence of such conceptions is revealed through the pattern of metaphors we use in texts and conversation. In particular, he points to the centrality of the metaphors of path and journey for logical reasoning or deduction.
Descriptions of proof include figures of speech reflecting this underlying metaphor. A proof has a "starting point", followed by "proof steps" "to reach" the "intended endpoint". Thus a proof can be interpreted as a cyclical journey. My claim is that this is part of a deep and shared meaning of all proof structures.
In modern English uses the term 'premises' is used both for the assumptions of a proof, and for a house, which is presumably the starting point of most journeys. This fits well with the metaphor of proof as journey. Etymologically, this double meaning of 'premises' does not arise from the metaphor. Historically the disposition of property in legal conveyancing was contained in the early section, the 'premises of the deed'. Through a metonymic shift, the term premises has become the general name of a building.
It needs to be made clear that the transformational narrative which is a proof need not consist of a straightforward transformation. While Lakatos' informal thought experiment proof is likely to be of this type, as is illustrated in the earlier proofs of the Euler Relation (Lakatos, 1976), more formal proofs can be rather more convoluted. They may, for example, assume the opposite of the theorem to be proved, and then proceed by the method of proof by contradiction. Although this particular form, proof by contradiction, is controversial to the extent that it is rejected by constructivists, Intuitionists, in particular, because it does not allow the theorem to be directly constructed.
Another analogue of cyclic transformation can be found in Alchemy, in which a common substance following complex (Al)chemical procedures is transformed into gold. Both of these types of narrative of transformation can be understood as allegorical accounts of spiritual enlightenment in which the initiate's mind goes on a voyage of self-discovery and returns, but transformed and elevated to a higher level (Jung, 1974). In other words, the cycle results in the acquisition of knowledge.
The features of the hero cycle resemble the story and myth analysis of the Russian formalists Propp and Todorov. Propp (1928) notes a shared formal structure and sequence of functions in many myths and folk-tales, which he claims all end in some form of gratified desire or successful quest. In the same way, all proofs seek through transformations to reach their intended and preordained endpoint, the theorem to be proved. Thus a partial analogy between proofs and such structures can be noted. Propp describes archetypal characters who appear in tales as hero, villain, dispatcher, false hero, donor, helper, princess, father. Counterparts of many of these characters occur in Campbell's Hero Cycle. Of course mathematical proofs do not have personal characters. So to press the metaphor I have to use what might be termed the 'reverse allegorical function': converting characters into abstract objects and concepts or expressions. Similarly (but oppositely), in allegories such as Buchan's Pilgrim's Progress, abstract objects concepts or terms are turned by an 'allegorical function' into persons, places and other concrete particulars.
What we call the beginning is often the end
And to make an end is to make a beginning.
The end is where we start from.
...
We shall not cease from exploration
And the end of all of our exploring
Will be to arrive where we started
And to know the place for the first time.
Eliot (1944: 42-3)
The interdependence of ends and beginnings in narratives is stressed by Young.
In a mathematical proof, the theorem is first stated as a conjecture, or statement-to-be-proved, and then after a transformational sequence or journey it reappears, justified and enhanced. Furthermore, to achieve the desired endpoint, the journey to it must be constructed with that end in mind. So the end informs the beginning, and all the subsequent stages. Overall, the beginning is indeed the end, and by the end there is new knowledge of the beginning.
There is thus a parallel between Campbell's hero myth cycle and mathematical proof , which can be brought out, using the stages in Young theory of narrative.
The parallel is good in many points, and weak in others. Thus the hero myth cycle could be matched with the tale in the Taleworld, but this would reduce the significance of the threshold crossing, and its parallel with the move from the level of signifiers to the realm of signifieds. The parallel also leaves a number of questions unanswered. Such as, what is a proof about? Beyond its structure, what is its subject matter or subject? Is there an analogue to the hero?
A mathematician reading mathematics also creates an agent: a mindless, unreflective automaton which is the tiniest identity within the of Chinese box of identities created, and when the text says "let ...", or "we sum this to infinity", it is this little agent who zips off in his imagined space, and carries out these actions. In doing mathematics we learn to create agents, and we are persuaded by the imagined actions of these agents. Rotman argues that proofs are fundamentally claims about what an agent can do under the circumstances laid out, and also series of instructions, or programmes, and the reader has to imagine the agent going through the prescribed actions.
A convincing proof is one in which the constructions, passages, imagined transformations seem to inevitably achieve the required and predicted end result.
Where is the hero? There is nobody in a proof, it is an empty formal structure, so how can there be a hero or any character? The hero is the wave-front of the readers attention as it progresses through the proof. It may be in the form of mathematician, reading the text and imagining the virtual space it signifies. It may be in the form of the agent carrying out the imagined procedures, etc., of the text. There is no hero in the text until the mathematician-reader passes the text through his/her mind, or rather passes his/her mind through the text.
Brouwer, L. E. J. (1913) Intuitionism and Formalism, in Benacerraf, P. and Putnam, H. Eds (1964) Philosophy of Mathematics: Selected readings, Englewood Cliffs, New Jersey: Prentice-Hall, 66-77.
Campbell, J. (1956) The Hero with a Thousand Faces, Cleveland: Meridian Books.
Eliot, T. S. (1944) The Four Quartets, London: Faber.
Ernest 1991, Ernest, P. (1991) Philosophy of Mathematics Education, London: Falmer Press.
Ernest, P. (1993) Mathematical Activity and Rhetoric: Towards a Social Constructivist Account, in I. Hirabayashi, N. Nohda, K. Shigematsu, F. L. Lin, Eds, Proceedings of PME-17 Conference, Tsukuba, Japan: University of Tsukuba, Volume 2, 238-245.
Ernest, P. (1994) The dialogical nature of mathematics, in Ernest, P. Ed. Mathematics, Education and Philosophy: An International Perspective, London, The Falmer Press, 1994, 33-48.
Hersh, R. (1993) Proving is Convincing and Explaining, Educational Studies in Mathematics, 24 (4) 389-399.
Jacobsen, T. (1946) Mesopotamia (chapters 5-7), in Frankfurt, H., Frankfurt, H. A., Wilson, J. A. and Jacobsen, T. (1946) Before Philosophy, London: Pelican Books.
Johnson, M. (1987) The Body in the Mind, Chicago: University of Chicago Press.
Jung, C. G. (1974) Dreams (trans. R. F. C. Hull), Princeton, N. J.: Bollingen Series, Princeton University Press.
Lakatos, I. (1976) Proofs and Refutations, Cambridge: Cambridge University Press.
Lyotard, J. F. (1984) The Postmodern Condition: A Report on Knowledge, Manchester: Manchester University Press.
Munitz, M. K. (1957) Theories of the Universe, New York: Free Press.
Propp, V. I. (1928) Morphology of the Folk Tale, (Translation published University of Texas Press, 1958).
Rotman, B. (1993) Ad Infinitum The Ghost in Turing's Machine: Taking God Out of Mathematics and Putting the Body Back in, Stanford California: Stanford University Press.
Smyth, J. V. (1995) A Glance at SunSet, in Smith, B. H. and Plotnitsky, A. Eds Mathematics, Science and Postclassical Theory, Special issue of The South Atlantic Quarterly, 94 (2) 619-654.
Snow, C. P. (1959) The Two Cultures and the Scientific Revolution, Cambridge: Cambridge University Press.
Tymoczko, T. Ed. (1986) New Directions in the Philosophy of Mathematics, Boston: Birkhauser.
Young, K. G. (1987) Taleworlds and Storyrealms, Dordrecht: Martinus Nijhoff.